This is a description of an “artificial river”, which is a mechanical construction for lifting up a container with water while a weight G is falling into a big box, which is standing in a big bath with water. The water in the container can be dropped into the reservoir of a waterturbine to generate energy. The weight G can be lifted again by the buoyancy. This can be repeated without external energy input. The computations are only theoretical at this moment. There are not yet experiments. Questions and remarks are welcome. (Text is in Dutch)

De constructie betreft een katrol, waarover een touw loopt met aan de ene kant een gewicht G met een soortelijke massa kleiner dan de helft van de soortelijke massa van water en aan de andere kant een container, die gevuld kan worden met water. Het gewicht G kan in een vat V zakken, dat uitsluitend lucht bevat, maar gelegen is in water, waarbij de bovenkant van het vat zich boven het wateroppervlak bevindt. Als het gewicht G zakt, wordt de container met water ophoog gehesen. Op deze manier kan het reservoir van een waterturbine worden gevuld. Een deel van de hoogte van het gewicht G moet echter gebruikt worden om mechanische arbeid bij andere vaten in het totale complex met meerdere vaten te verrichten.

Een vat heeft de vorm van een dubbele piramide als het in het water wordt gelaten (zie figuur 2), waarbij de massa van het vat groter is dan het volume van het (dichtgeklapte) vat x de soortelijke massa van water. Het vat zinkt daardoor in het water tot dat er een bevestiging aan 4 palen in het water tot stand komt. Het vat V kan van boven geopend worden, waarbij de zijkanten van de bovenste helft van de piramide openklappen, zonder dat er water in het vat kan komen. Het vat V moet opengebroken worden voordat het gewicht G in het vat kan zakken. Daarbij krijgt het vat de vorm zoals in figuur 1 en heeft een volume binnen het omhulsel van het vat, zodat het vat zou gaan drijven.(zonder vulling met extra gewicht) Doordat het vat echter vastzit aan palen, gaat het niet drijven, maar vangen de palen de opwaartse kracht op. De afmetingen van het vat in de berekeningen zijn: lengte van het middenvlak 2m, breedte van het middenvlak 1m, hoogte in totaal 20m.

Het gewicht van het vat moet ongeveer 13.500 kg zijn om het te laten zinken.

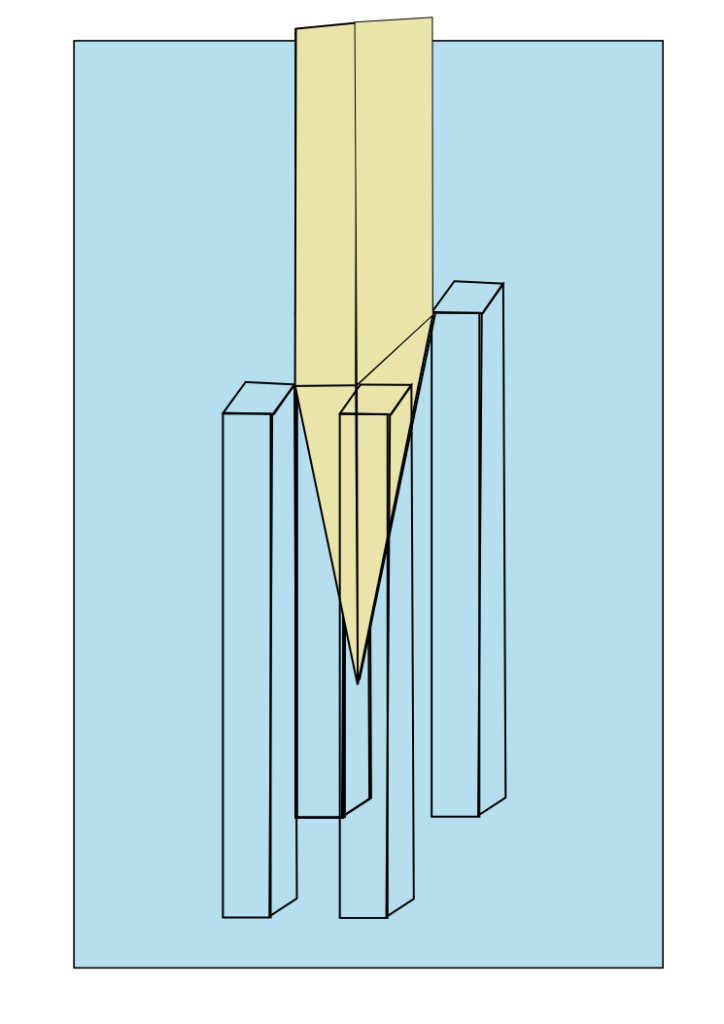
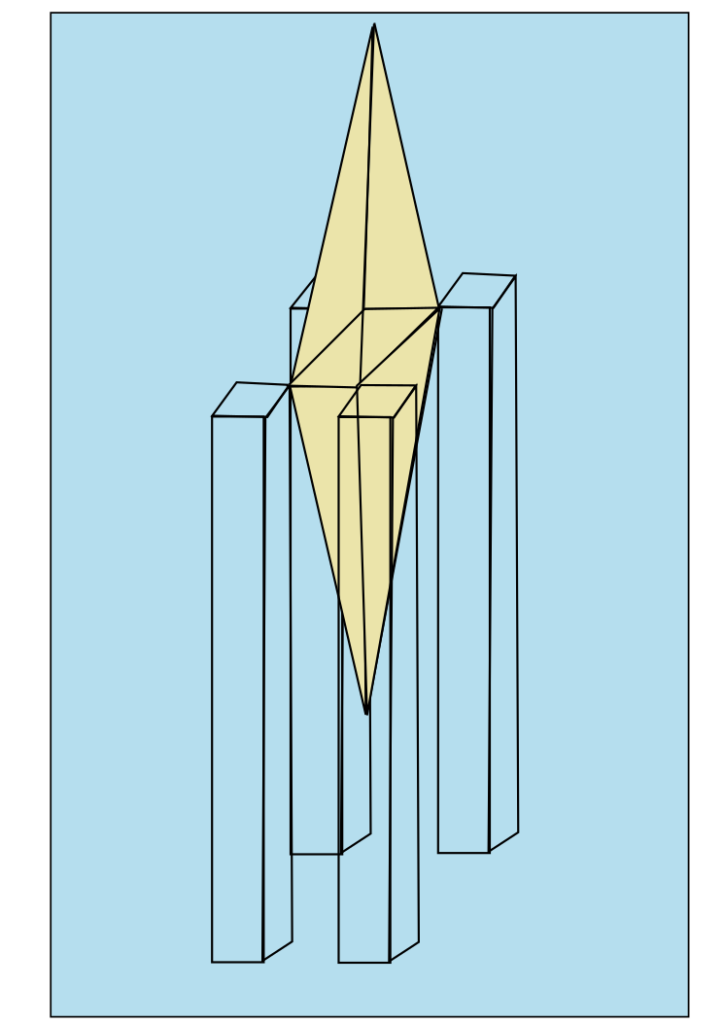
Het openbreken van het vat

Het vat moet opgebroken worden met een deel van de hoogte-energie van het gewicht G dat bij een ander vat hoort.

Beschouw voor de berekeningen de balk B met zijden 2m, 1m en 20 m. Het volume water dat verplaatst moet worden bij het openen van het vat V, is 1/3 van het volume van de balk B en heeft totaalgewicht van 13.333 kg.

Als het vat opengebroken is, heeft het een volume van 2/3 van de zojuist beschreven balk. De massa van het gewicht G (behorend bij dat vat) kan het hele opgebroken vat vullen. Het soortelijk gewicht wordt 0,45 van het soortelijk gewicht van water genomen.

De massa van een gewicht G met een volume van 2/3 van de zojuist beschreven balk en soortelijke massa gelijk aan 0,45 van de soortelijke massa van water is gelijk aan 12000 kg. Met dit gewicht moet de bovenste helft van de piramide opengebroken worden. Dit gebeurt met een tweede katrol, waar aan de ene kant het gewicht G bevestigd is en aan de andere kant de bevestiging plaatsvindt in het zwaartepunt van elk van de zijvlakken en hoekconstructies, die de bovenste helft van de dubbele piramide begrenzen.

Er bevinden zich naar binnen geklapte constructies in de hoeken, zodat als deze opengeklapt zijn, het bovenste deel van het vat over de hele hoogte een zelfde horizontale doorsnede krijgt van 2m x 1 m.

De vraag is hoe ver het gewicht moet zakken, om het vat open te breken, zodat de zijvlakken van het bovenste deel van de dubbele piramide in verticale stand komen te staan.

De totale kracht op het grote driehoekige zijvlak van het vat (denkbeeldig gesitueerd in het zwaartepunt) is maximaal:

(waarin α de hoek is die het zijvlak met het horizontale vlak maakt).

Omdat het zwaartepunt van een piramide zich op ¼ van de hoogte bevindt, bevindt het zwaartepunt van het te verplaatsen water zich op 15/24 van de hoogte van de piramide.

We gaan er echter van uit, dat het zwaartepunt van elk van de zijvlakken op 1/3 van de hoogte, dus op 3,33 m onder het wateroppervlak ligt.

De afstand waarover het zwaartepunt van het grote zijvlak verplaatst moet worden is ongeveer 35 cm voor de grote zijvlakken en 70 cm voor de kleine zijvlakken.

Uitgaande van 70 cm per vlak, waarvoor 3000 kg gewicht beschikbaar is en waarmee 5000 kg overwonnen moet worden, zou het gewicht (met verwaarlozing van wrijving) 117 cm moeten zakken.

De vraag is of het laten zakken van het gewicht tot 2,5 m (meer dan 2 x zo veel!) voldoende is om de constructie te laten werken.

Nadat het vat opgebroken is, kan het gewicht G in delen in het vat zakken, waarbij een deel van de zwaarte-energie gebruikt wordt om een zelfde gewicht weer 2,5 meter op te heffen, maar de rest gebruikt kan worden voor het opheffen van een container met water.

Het water van de container wordt geloosd in een waterturbine, waardoor energie wordt omgezet in elektriciteit.

Zinken en stijgen

Om het vat niet te ver te hoeven opheffen, laten we het vat horizontaal in het water dalen. Hiervoor wordt het grootste deel van het gewicht van het vat in het midden aan een kant van het vat bevestigd. Hierdoor kunnen de zijkanten van het vat zo licht mogelijk zijn, zodat dit bij het opentrekken van het vat ook een aanzienlijke reductie van het te verplaatsen gewicht geeft.

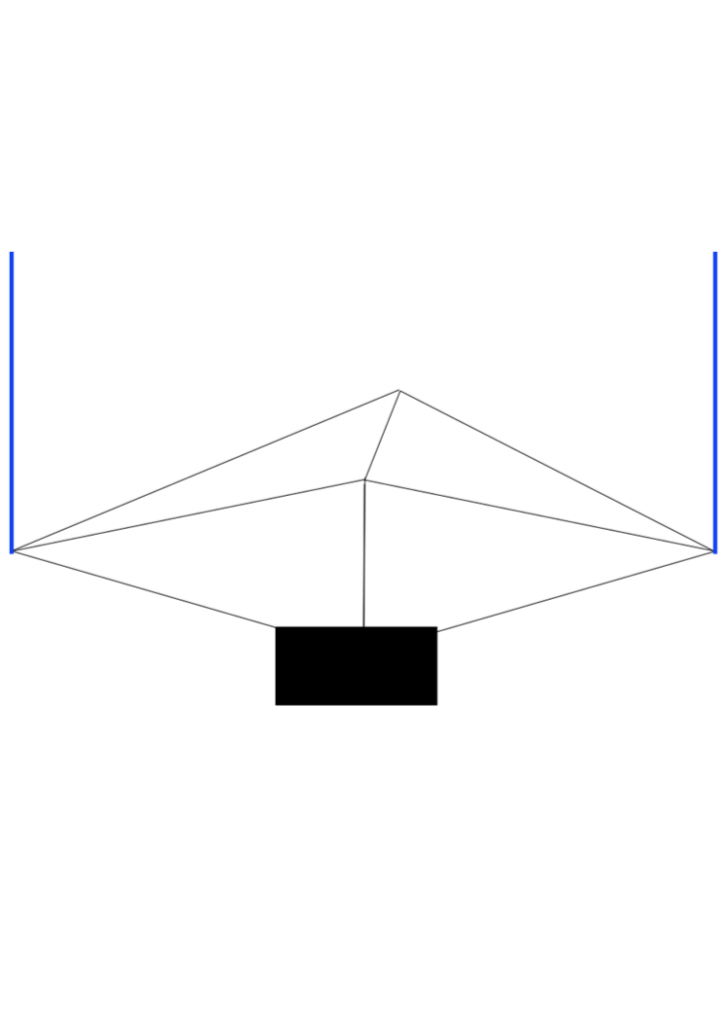
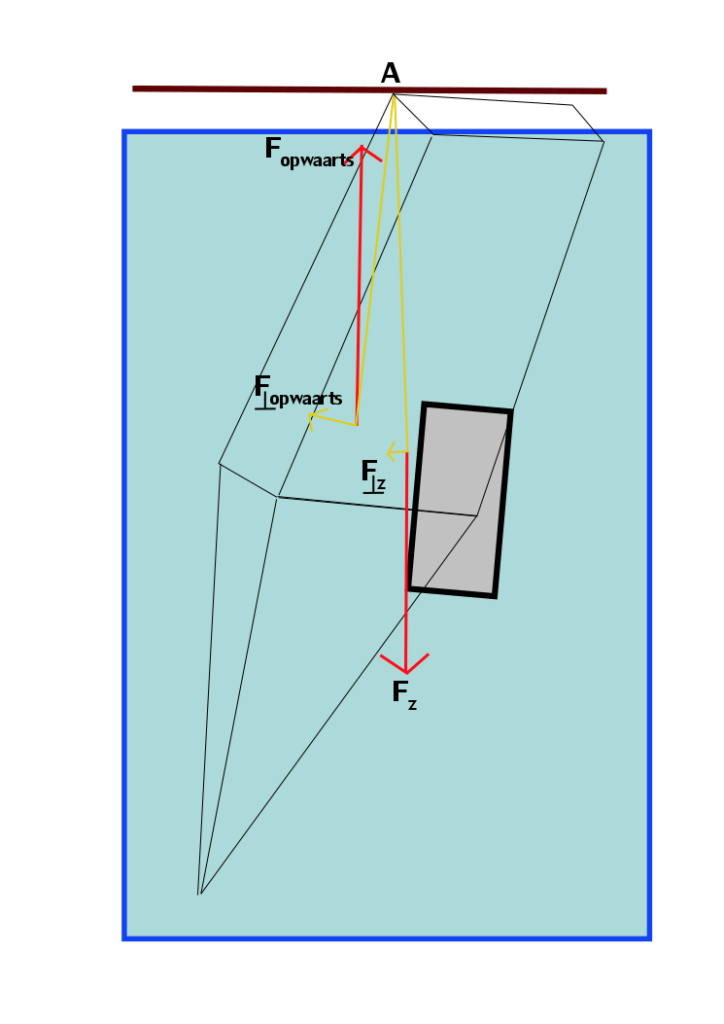
Aan de blauwe touwen kan het vat gecontroleerd zakken in het water. Als het vat tot een diepte gelijk aan de halve hoogte van het vat onder water is kan het met weinig energie in verticale stand gedraaid worden, omdat de totale opwaartse kracht op het vat steeds gelijk blijft en er ook geen zwaartekracht overwonnen hoeft te worden. Eventueel is er een klein extra gewicht aan de kant van het vat dat naar beneden draait.

Nadat het vat geopend is aan de bovenzijde en gevuld met gewicht, kan het vat losgemaakt worden en gaat het stijgen. Er moet echter voor gezorgd worden dat het vat horizontaal (met de lengte van het vat langs het wateroppervlak) komt te liggen. Hiertoe moet het draaikoppel naar boven gericht zijn vanuit het draaipunt A in onderstaande afbeelding. Er wordt hier vanuit gegaan dat de opwaartse kracht aangrijpt in het meetkundig zwaartepunt van het vat. Eventueel wordt de vulling aan de onderzijde van het vat iets lichter gemaakt dan aan de bovenzijde. (Dan wordt de arm naar het aangrijpingspunt van de zwaartekracht korter) Omdat de armen van het draaikoppel naar F_z en F_opwaarts weinig schelen in lengte en F_z en F_opwaarts maximaal een factor 2 schelen (in het geval dat het vat opengetrokken is en niet gevuld), is er een positief koppel mogelijk met draaipunt A. De conclusie is dus dat als door plank P het gevulde vat, nadat het losgelaten is, niet door verticale stijging F_z en F_opwaarts gelijk kan krijgen, het vat zal gaan draaien rondom punt A totdat er voldoende volume van het vat zich boven het water bevindt. Als punt A zich dicht genoeg op het water bevindt, zal het vat horizontaal komen te liggen.